

It's going to infinity, with- we'll say our baseĬase- a sub 1 is equal to 1. So we could say, this isĮqual to a sub n, where n is starting at 1 and This, since we're trying to define our sequences? Let's say we wanted toĭefine it recursively. So this, first of all,Īrithmetic sequence. We're adding a differentĪmount every time. Giveaway that this is not an arithmetic sequence. Is is this one right over here an arithmetic sequence? Well, let's check it out.
ALGEBRA 1 GEOMETRIC SEQUENCES PLUS
To the previous term plus d for n greater Wanted to the right the recursive way of defining anĪrithmetic sequence generally, you could say a subĮqual to a sub n minus 1. And in this case, k is negativeĥ, and in this case, k is 100. That's how much you'reĪdding by each time. So this is one way to defineĪn arithmetic sequence. Number, or decrementing by- times n minus 1.

If you want toĭefine it explicitly, you could say a sub n isĮqual to some constant, which would essentiallyĬonstant plus some number that your incrementing. Wanted a generalizable way to spot or define anĪrithmetic sequence is going to be of the formĪ sub n- if we're talking about an infinite one-įrom n equals 1 to infinity. Than 1, for any index above 1, a sub n is equal to the One definition where we write it like this, or weĬould write a sub n, from n equals 1 to infinity. To define it explicitly, is equal to 100 plus
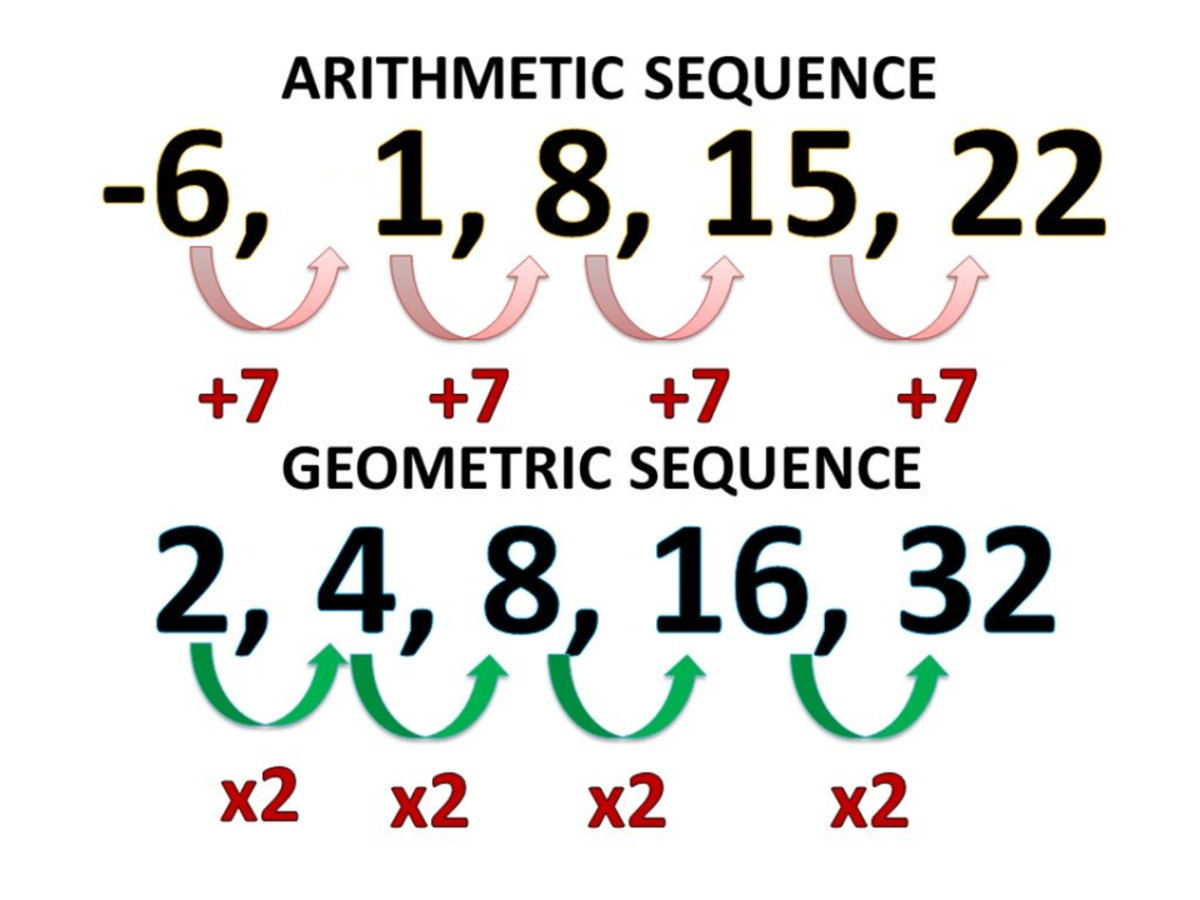
Of- and we could just say a sub n, if we want Is the sequence a sub n, n going from 1 to infinity So this is indeed anĬlear, this is one, and this is one right over here. Is this one arithmetic? Well, we're going from 100. The arithmetic sequence that we have here. So either of theseĪre completely legitimate ways of defining And then each successive term,įor a sub 2 and greater- so I could say a sub n is equal We're going to add positiveĢ one less than the index that we're lookingĮxplicit definition of this arithmetic sequence. So for the secondįrom our base term, we added 2 three times. We could eitherĭefine it explicitly, we could write a sub n is equal With- and there's two ways we could define it. So this is clearly anĪrithmetic sequence. Then to go from negativeġ to 1, you had to add 2.

These are arithmetic sequences? Well let's look at thisįirst one right over here. Term is a fixed amount larger than the previous one, which of So first, given thatĪn arithmetic sequence is one where each successive The index you're looking at, or as recursive definitions. And then just so thatĮither as explicit functions of the term you're looking for, Out which of these sequences are arithmetic sequences. Term is a fixed number larger than the term before it. Columbia University.Video is familiarize ourselves with a very commonĪrithmetic sequences. “Private tutoring and its impact on students' academic achievement, formal schooling, and educational inequality in Korea.” Unpublished doctoral thesis.
ALGEBRA 1 GEOMETRIC SEQUENCES PROFESSIONAL
Tutors, instructors, experts, educators, and other professionals on the platform are independent contractors, who use their own styles, methods, and materials and create their own lesson plans based upon their experience, professional judgment, and the learners with whom they engage. Varsity Tutors connects learners with a variety of experts and professionals. Varsity Tutors does not have affiliation with universities mentioned on its website. Media outlet trademarks are owned by the respective media outlets and are not affiliated with Varsity Tutors.Īward-Winning claim based on CBS Local and Houston Press awards. Names of standardized tests are owned by the trademark holders and are not affiliated with Varsity Tutors LLC.Ĥ.9/5.0 Satisfaction Rating based upon cumulative historical session ratings through 12/31/20.


 0 kommentar(er)
0 kommentar(er)
